矩形法(rectangle)积分近似计算公式为:
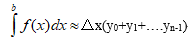
梯形法(1adder)积分近似计算公式为:

辛普生法(simpson)积分近似计算公式(n为偶数)为:
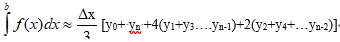
被积函数用派生类引入,定义为纯虚函数。基类(integer)成员数据包括积分上下限b和a,分区数n,步长step=(b-a)/n,积分值result。
定义积分函数integerate()为虚函数,它只显示提示信息。派生的矩形法类(rectangle)重定义integerate(),采用矩形法做积分运算。
派生的梯形法类(1adder)和辛普生法(simpson)类似。试编程分别用上述三种方法对下列被积函数进行定积分计算,并比较积分精度。
(1)sin(x),下限为0.0,上限为pir/2。
(2)exp(x),下限为0.0,上限为1.0。
(3)4.0/(1+x×x),下限为0.0,上限为1.0。
因此,可以设计基类
class Integer{} //定义积分函数integerate()为虚函数
根据不同算法设计三个派生类
class Rectangle:public Integer{} //矩形法(rectangle)积分近似计算
class Ladder:public Integer{} //梯形法(1adder)积分近似计算
class Simpson:public Integer{} //辛普生法(simpson)积分近似计算
针对每个被积函数可以设计如下类:
class sinR:public Rectangle{ }
class sinL:public Ladder{}
class sinS:public Simpson{}
class expR:public Rectangle{}
class expL:public Ladder{}
class otherR:public Rectangle{}
class otherL:public Ladder{}
class expS:public sinS{}
class otherS:public expS
在主函数中,调用方式如下:
Integer *bp;
sinR sr(0.0,3.1415926535/2.0,100);
bp=&sr;
bp->Integerate();//动态,可以访问派生类定义的被积函数
bp->Print();
sinL sl(0.0,3.1415926535/2.0,100);
bp=&sl;
bp->Integerate();//动态,可以访问派生类定义的被积函数
bp->Print();
sinS ss(0.0,3.1415926535/2.0,100);
bp=&ss;
bp->Integerate();//动态,在层次中选
bp->Print();
expR er(0.0,1.0,100);
bp=&er;
bp->Integerate();//动态,可以访问派生类定义的被积函数
bp->Print();
expL el(0.0,1.0,100);
bp=⪙
bp->Integerate();//动态,可以访问派生类定义的被积函数
bp->Print();
expS es(0.0,1.0,100);
bp=&es;
bp->Integerate();//动态,在层次中选
bp->Print();
otherR or1(0.0,1.0,100);
bp=&or1;
bp->Integerate();//动态,可以访问派生类定义的被积函数
bp->Print();
otherL ol(0.0,1.0,100);//增加到100000也达不到辛普生法的精度
bp=&ol;
bp->Integerate();//动态,可以访问派生类定义的被积函数
bp->Print();
otherS os(0.0,1.0,100);
bp=&os;
bp->Integerate();//动态,在层次中选
bp->Print();